Neodymium Temperature Ratings
The Original Online Magnet Company
Temperature Effects on Neodymium Iron Boron, NdFeB, magnets
The NdFeB magnets are the strongest magnets available. Up to +150 degrees C, they are stronger than the other Rare Earth magnet, SmCo. At around +150 degrees C and above these Neo magnets perform not as strongly as SmCo. The maximum recommended temperature for the NdFeB magnets is +230 degrees C, whereas the SmCo can work at +300 to +350 degrees C.
NdFeB can be used at low temperature but at around 135 Kelvin (-138 degrees C), the direction of magnetisation is said to change from a single axis (easy-axis) to an easy-cone which could cause a fall in output of up to 15% due to this spin reorientation. It is possible to use Neodymium Iron Boron magnets to be used at even colder temperatures but this drop in output will need to be taken into account.
The temperature coefficient of Intrinsic Coercivity (how Hci varies with temperature), b, for Neodymium is approximately -0.6%/degree C (from ambient, but a range of -0.45%/degree C to -0.6%/degree C is possible depending on the Neodymium grade) between +20 and +120 degrees C.
The temperature coefficient of Remanent Induction (how Br varies with temperature), a, for Neodymium is -0.12%/degree C (from ambient, but a range of -0.08%/degree C to -0.12%/degree C is possible depending on the Neodymium grade).
It should be noted that, strictly speaking, these values for a and b actually vary with temperature and use of stated values beyond 20 to 120 degrees C may result in inaccuracies when designing (actual BH curves at temperatures assist in clarifying for design purposes).
Temperature Characteristics of NdFeB Grades
| MAGNET TYPE SUFFIX | Rev.Temp.Coef. of Induction (Br), a, %/°C (20-100°C) | Rev.Temp.Coef. of Coercivity (Hci), b, %/°C (20-100°C) | Max. Working Temperature |
| (based on High working point) | |||
| -0.12 | -0.6 | 80 ºC = 176 ºF * | |
| M | -0.12 | -0.58 | 100ºC = 212 ºF |
| H | -0.11 | -0.58 | 120ºC = 248 ºF |
| SH | -0.1 | -0.55 | 150 ºC = 302 ºF |
| UH | -0.09 | -0.52 | 180 ºC = 356 ºF |
| EH | -0.085 | -0.5 | 200 ºC = 392 ºF |
| VH / AH | -0.08 | -0.45 | 230 ºC = 446 ºF |
| * 60 ºC for N50 and N52 |
There are three effects due to elevated temperatures.
A reversible loss is when the output falls with temperature but returns as it cools down (the temperature coefficients reflect this e.g. a twenty-degree C rise above ambient causes a drop in magnetic output of N42 of around 20 x 0.12 = 2.4%, which recovers when the temperature returns down to ambient).
An irreversible but recoverable loss occurs when the output falls but does not return when the magnet cools down (e.g. the high temperature takes the Intrinsic working point beyond the knee of the Intrinsic curve, causing demagnetisation) but this would be recovered if the Neodymium magnet is remagnetised.
For all extents and purposes, this output is lost because the magnet will not be remagnetised during practical application but will demagnetise again if a remagnetised magnet is re-used in the same application (the heat will demagnetise the Neodymium magnet again - the magnetic circuit would have to be improved to fix this problem).
When cooled, such a demagnetised magnet will have the original Hci but a lower Br (the Br will have increased by the reversible temperature coefficient amount applied to the reduced high-temperature Br).
An irreversible irrecoverable loss is due to a high temperature causing a permanent structural change in the magnet as is usually because the magnet has been taken far beyond its working temperature. The damage is permanent and remagnetising will not bring the performance back again.
If an irreversible but recoverable loss occurs, the magnet is said to be thermally stabilized. If the cooled Neodymium magnet is taken back up to temperature, no further irreversible losses will occur – the only loss is the temporary drop in output due to the reversible losses (a function of the temperature coefficients). By being thermally stabilized, the Neodymium magnetic performance is better predicted even if the drop in output has occurred due to an irreversible but recoverable loss.
Some applications may require this thermal stabilization which is usually done by taking to a temperature a few degrees C above the required maximum operating temperature but it may also be performed by applying a demagnetising pulse (this replicates the process by taking the Intrinsic curve beyond the knee of the Intrinsic curve but requires knowing by how much the magnets would demagnetise by through raised temperature but cannot take into account BH curve waveshape variations so has an element of inaccuracy at all times).
It is also generally advised against subjecting magnets to thermal shock (i.e. putting a cold magnet onto an extremely hot surface) as too high a thermal shock could cause the magnets to break.
How Grade Choice Affects Performance When the NdFeB Magnet is Subjected to Heat
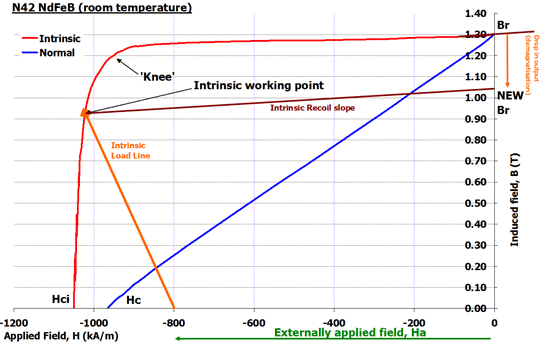
It is possible to demagnetise a Neodymium magnet by applying an external magnetic field in a direction opposite to the direction of magnetisation (DoM) of the NdFeB magnet. The extent of demagnetisation is a function of the total magnetic circuit (and hence the Intrinsic working point), the temperature (and hence the actual BH curve shape for the NdFeB in use) and the magnitude of the externally applied demagnetising field.
If the Intrinsic working point is known, a line drawn on the BH curve from the origin (B=0, H=0) to the Intrinsic working point is drawn (this is the Intrinsic Load Line). If the magnitude of the externally applied demagnetising field is known (Ha), the Intrinsic Load Line is translated along so the start of the load line has moved from H=0 to H=Ha.
The slope of the load line is the same but the working point in the Intrinsic curve has moved. If the new Intrinsic working point has not entered the region of the ‘knee’ of the Intrinsic curve, the demagnetisation of the magnet is minimal, possibly so little it cannot be measured. When the external field is removed, the Intrinsic working point ‘recoils’ back but at a slope equal to the Intrinsic curve slope where H=0 and B=Br. If the Intrinsic working point had entered the region of the ‘knee’, the recoil does not follow the original BH curve shape – a new BH curve shape is produced which has a lower new Br (this is the effect of demagnetisation).
Applying an external field again up to the same magnitude as the original Ha has no further demagnetising effect – only if Ha exceeds the original Ha will further demagnetisation be seen. If the Ha equals Hc (the coercive force), the Neodymium magnet will appear to have no magnetic output whilst the field is applied but removing the field will have caused potentially very high demagnetisation. But if Ha equals Hci (the Intrinsic coercive force, when Ha is removed, the Neodymium magnet will be totally demagnetised (i.e. it will show no magnetic performance).
To minimize the effects of externally applied fields, higher Hci rated Neodymium magnets may be used and the design can be improved to give a better Intrinsic Load Line (also known as a higher Pci or Intrinsic Permeance Coefficient, where Pci=Pc+1 and Pc is the Permeance Coefficient based on using the Normal Curve). Where possible a lower operating temperature for the application may also assist (this is unlikely to be designed in though).
How a Magnet is Demagnetised by Applying an External Magnetic Field
It is possible to demagnetise a Neodymium magnet by applying an external magnetic field in a direction opposite to the direction of magnetisation (DoM) of the NdFeB magnet. The extent of demagnetisation is a function of the total magnetic circuit (and hence the Intrinsic working point), the temperature (and hence the actual BH curve shape for the NdFeB in use) and the magnitude of the externally applied demagnetising field.
If the Intrinsic working point is known, a line drawn on the BH curve from the origin (B=0, H=0) to the Intrinsic working point is drawn (this is the Intrinsic Load Line). If the magnitude of the externally applied demagnetising field is known (Ha), the Intrinsic Load Line is translated along so the start of the load line has moved from H=0 to H=Ha. The slope of the load line is the same but the working point in the Intrinsic curve has moved.
If the new Intrinsic working point has not entered the region of the ‘knee’ of the Intrinsic curve, the demagnetisation of the magnet is minimal, possibly so little it cannot be measured. When the external field is removed, the Intrinsic working point ‘recoils’ back but at a slope equal to the Intrinsic curve slope where H=0 and B=Br. If the Intrinsic working point had entered the region of the ‘knee’, the recoil does not follow the original BH curve shape – a new BH curve shape is produced which has a lower new Br (this is the effect of demagnetisation).
Applying an external field again up to the same magnitude of the original Ha has no further demagnetising effect – only if Ha exceeds the original Ha will further demagnetisation be seen. If the Ha equals Hc (the coercive force), the Neodymium magnet will appear to have no magnetic output whilst the field is applied but removing the field will have caused potentially very high demagnetisation. But if Ha equals Hci (the Intrinsic coercive force, when Ha is removed, the Neodymium magnet will be totally demagnetised (i.e. it will show no magnetic performance).
To minimize the effects of externally applied fields, higher Hci rated Neodymium magnets may be used and the design can be improved to give a better Intrinsic Load Line (also known as a higher Pci or Intrinsic Permeance Coefficient, where Pci=Pc+1 and Pc is the Permeance Coefficient based on using the Normal Curve). Where possible a lower operating temperature for the application may also assist (this is unlikely to be designed in though).
For note, the effects of temperature and external demagnetising fields are easiest to calculate on NdFeB magnets that may be demagnetised as a result of such exposure if cgs units are used (Gauss, Tesla, MGOe) as cgs units allow faster production of new BH curves.
When a new Intrinsic BH curve for Neodymium has been calculated (due to demagnetisation), at any point on the Intrinsic curve, note the corresponding value of H in Oersted and remove it from the corresponding B (in Gauss) of the Intrinsic curve and the resulting value is that of the value of B on the Normal curve (in Gauss) for the same H value.
Using this, the Normal BH curve at different temperatures can be estimated if you already have an accurate ambient temperature BH curve for the “Neo” magnet (although this can be applied to any magnet material).
Note the Br and Hci at ambient temperature (20 degrees C). If you want the curve at e.g. 120 degrees C, take the ambient temperature away to get the temperature difference (i.e. 120-20=100 degrees C). Multiply this result by the temperature coefficients to give the percentage changes in Br and Hci to be expected. So Br will drop by 100x-0.12=-12% and Hci will drop by 100*-0.6 = 60%. Translate the Intrinsic BH curve shape so the curve starts and ends at the newly calculated Br and Hci and re-draw the new Intrinsic curve. This is the Intrinsic curve at 120 degrees C. Then use the calculation to convert from Intrinsic to Nomal in cgs units for any given H in Oersteds to generate the new Normal curve for the NdFeB. This new BH curve set can then be used for the calculations at 120 degrees C.
Please note that this is an estimate as the temperature coefficients actually vary with temperature and the BH curve varies from batch to batch for any magnet, including Neodymium.
Discover More
Get in touch today
Please do not hesitate to contact us with any question or query you may have. Our professional team will give you expert advice and guidance for your magnetic application and equipment.


